Check out my new gamedev blog!

Hop over to www.lewismoronta.com to check out game development articles and graphics programming in general.

Halloween Special: How to Draw Spooky Spiderwebs in JavaScript!

I Got a New Microphone: Blue Yeti

...so naturally, here's an unboxing in stop-motion :)

CGS Head Rig Animation

Hey everyone! I want to share my latest animation. I rigged the head over several weeks and animated it in the past few days. I haven't worked on any corrective blends yet so I'm still open to critiques. The animation is meant to push the limits of the rig. Thanks for watching!

Angle Based Deformers

What I am about to talk about is closely related to Pose Space Deformers--I’m sure you can find the original SIGGRAPH PSD papers online. However, the setup I present below is a simple network that allows you to trigger actions and/or blends based on the angle between two vectors. Vectors save the day once again…

Why ditch Euler angles when we already have angle positions?? Because of the nature of Eulers, the X, Y, and Z components are calculated in a specific way that won’t work in many situations. One of the main reasons for this is Gimbal Lock. This one reason can make things a living nightmare for us.
Using the dot product, we can find the angle between two vectors, A and B, by using the following equation:

Θ = acos(A · B)

This means that if we were to attach a locator to a pair of adjacent joints, where both locator’s origin is positioned where the joints connect, you can find the arc cosine of the dot product of both of these vectors, and return the angle between them. I know… it sounds wordier than it really is.

Here’s how I set this up in Maya:


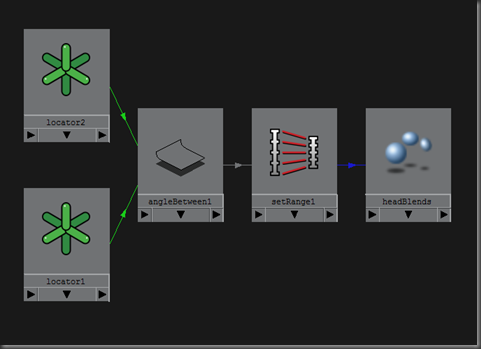
To be able to see the results of my network, I attached the output of setRange to a blendshape channel. I then animated the joint driving the location of a locator to get a change in the angle between locator1 and locator2. Maya’s angleBetween node returns 0-180, so I scaled that value down to 0 to 1 using the setRange node.

We could have just as easily used an expression to put this example together. However, I prefer to stay away from expressions for anything that I can build using nodes. Native nodes evaluate faster and you can’t break their dependencies by duplicating the network or changing their names!

I hope you can find many uses for this angle based setup. Let me know what you come up with!

NURBS Curves: How to use Knot Vectors

When working in Maya, we create curves freely without crunching numbers. We use them in Maya Hair, Spline IK rigs, Motion/Flow paths, as control curves for characters rigs, create them procedurally for modeling, amongst other uses. My goal in this post is for you to better understand how to generate curves using knot vectors.

---

Linear curves are simply lines that follow the standard y = mx + b formula. In Maya, they are created as a curve of 1 degree. That means that the highest power in the equation is 1. In theory, this curve type has 2 knots. The relation between knots to CV is: #knots = (#CVs+deg -1).

string $curve = `curve -d 1 -p -2 0 0 -p 2 0 -2`;

Simply pass in your two points, and tell Maya that you’re drawing a linear curve. Let’s attach a curveInfo node to this curve and poke around a little bit.

string $cInfo = `arclen -ch 1 $curve`;
getAttr($cInfo+".knots[*]");
// Result: 0 1 //
 
It seems that there are two knots on this curve that are weighted to each CV on the curve. Using #knots = (#CVs+deg -1), we know that we have 2 CVs on a curve of 1 degree, minus 1: that’s 2 knots. So we know that checks out.

Before we investigate further, let’s try the same thing with a quadratic curve. Behind the scenes, Maya will draw the smooth curve using an equation where the highest degree order is 2. Since we all miss our high school math classes, let’s draw a parabola:

$curve = `curve -d 2 -p -1 0 -2 -p -1 0 0 -p 1 0 0 -p 1 0 -2`;
$cInfo = `arclen -ch 1 $curve`;
getAttr($cInfo+".knots[*]");
// Result: 0 0 1 2 2 //
 
We have a curve of 2 degrees, we plotted 4 points, minus 1: that’s a total of 5 knots. The collection of knots on a curve is referred to its Knot Vector. However, what do these knot magnitudes mean? Each element in the vector determines where in parameter space the curve will be drawn. I know that’s a very vague statement but please stay with me!

Think of the first and last points on a curve as an anchor. This is the most common type of knot vector: Pinned Uniform Knot Vectors. Each anchor needs to be held down by the same number of knots as the curve’s degree. In our first example, we had a curve of 1 degree being pinned down by one knot on each end point. In our second example, we had a curve being held down by 2 knots on each end point.

So then what does the 1 mean in the [0 0 1 2 2] result? It turns out that these numbers are arbitrary. The number values don’t matter in a Knot Vector. Say what? Yes, that’s right. What matters is the ratios of the values to each other. The main rule is that Maya requires each knot’s magnitude to be in ascending order. So what happens if we create a curve but mess with that middle knot? What results will we get? Let’s try it!

curve -d 2 -p -1 0 -2 -p -1 0 0 -p 1 0 0 -p 1 0 –2
      -k 0 -k 0 -k 0 -k 2 -k 2;

By specifying the knot values to the curve command, it seems we have created a curve with non-uniform weighting. We modified the middle knot in a way that we made the curve appear discontinuous.

Just for fun, we can weight the center knot to the other end to get a mirrored result.

curve -d 2 -p -1 0 -2 -p -1 0 0 -p 1 0 0 -p 1 0 –2
      -k 0 -k 0 -k 2 -k 2 -k 2;

Go ahead and release the pins on this 2nd degree curve. Notice that you can easily un-anchor the curve from their start and end points by simply supplying different weights. This also makes your curve a lot shorter. This is something you need to try for yourself because it’s one of those things that are too abstract in words.

Uniformly distributing our knots makes our NURBS curve simply a B-Spline. Having the ability to specify and interactively adjust the knots is a feature of NURBS, or Non-Uniform Rational B-Splines. Allowing a partial knot weight is a nice feature:

curve -d 2 -p -1 0 -2 -p -1 0 0 -p 1 0 0 -p 1 0 –2
      -k 0 -k 0 -k 1.5 -k 2 -k 2;
curve -d 2 -p -1 0 -2 -p -1 0 0 -p 1 0 0 -p 1 0 –2
      -k 0 -k 0 -k 0.5 -k 2 -k 2;

Finally, to nail the point, let’s try drawing an pinned cubic curve with a degree of 3.

curve -d 3 -p -1 0 -3 -p -2 0 -2 -p 0 0 0 -p 2 0 -2 -p 1 0 –3
      -k 0 -k 0 -k 0 -k 1 -k 2 -k 2 -k 2;

Notice that I used 3 pinned knots to hold down the end points. The middle knot is exactly half way between 0 and 2. This makes the curve uniformly weighted. If you have questions, please let me know in the comment section! I’m sure there are things I can clarify. I want to be sure the information comes through clearly.

---

Notes:
- Maya seems to ignore knot magnitudes on linear curves.
- When creating curves with the -pointWeight flag, accurate knot values are not returned.
- When editing curves created with the -pointWeight flag in the viewport, the curves seem to snap to a weighted value of 1 to each CV.

A List of My Favorite Books

Several people have asked me about what resources I use to learn my favorite topics. There are informative videos and written tutorials scattered all over the web, and only but a few are concise, efficient, and well prepared. This is why I rely mostly on books that are written by seasoned professionals that know a thing or two about teaching. Here is a list of the books I am in love with:

• MEL Scripting for Maya Animators
• Mastering Autodesk Maya
• Stop Staring: Facial Modeling and Animation Done Right
• Maya Python for Games and Film
• Complete Maya Programming I & II
• Art of Rigging I & II
• Professional MEL Solutions for Production
• Maya Visual Effects: The Innovator's Guide
• 3D Math Primer for Graphics and Game Development
• Game Development with ActionScript

These gems are not listed in any particular order but MEL Scripting for Maya Animators was the first book I ever read on MEL, or Maya for that matter. I bought the very first edition of that text because I was looking for a source of inspiration when I was stuck at home writing Game Development with ActionScript. They are both considered oldies as far as technology goes, so they might be tough to find.