Angle Based Deformers

What I am about to talk about is closely related to Pose Space Deformers--I’m sure you can find the original SIGGRAPH PSD papers online. However, the setup I present below is a simple network that allows you to trigger actions and/or blends based on the angle between two vectors. Vectors save the day once again…

Why ditch Euler angles when we already have angle positions?? Because of the nature of Eulers, the X, Y, and Z components are calculated in a specific way that won’t work in many situations. One of the main reasons for this is Gimbal Lock. This one reason can make things a living nightmare for us.
Using the dot product, we can find the angle between two vectors, A and B, by using the following equation:

Θ = acos(A · B)

This means that if we were to attach a locator to a pair of adjacent joints, where both locator’s origin is positioned where the joints connect, you can find the arc cosine of the dot product of both of these vectors, and return the angle between them. I know… it sounds wordier than it really is.

Here’s how I set this up in Maya:


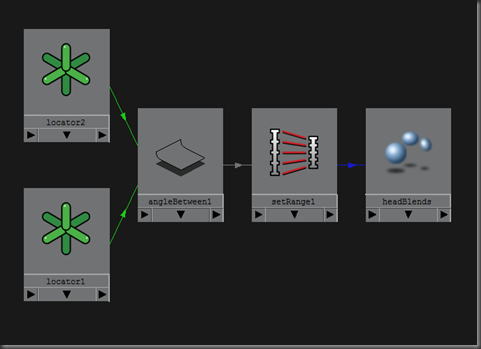
To be able to see the results of my network, I attached the output of setRange to a blendshape channel. I then animated the joint driving the location of a locator to get a change in the angle between locator1 and locator2. Maya’s angleBetween node returns 0-180, so I scaled that value down to 0 to 1 using the setRange node.

We could have just as easily used an expression to put this example together. However, I prefer to stay away from expressions for anything that I can build using nodes. Native nodes evaluate faster and you can’t break their dependencies by duplicating the network or changing their names!

I hope you can find many uses for this angle based setup. Let me know what you come up with!